最小生成树

并行 BGL 包含四种最小生成树 (MST) 算法 [DG98]，用于无向、加权、分布式图。图无需连通：当提供不连通图时，每种算法都将计算最小生成森林 (MSF)。

每种算法的接口都类似于顺序 BGL 中“Kruskal 算法”的实现。每个算法至少接受一个图、一个权重映射和一个输出迭代器。 MST（或 MSF）的边将通过进程 0 上的输出迭代器输出：其他进程可能会在其输出迭代器上接收边，但该集合可能不完整，具体取决于算法。算法参数一起记录，因为它们变化不大。有关算法选择的建议，请参阅选择 MST 算法部分。

图本身必须符合顶点列表图概念和分布式边列表图概念。由于最常见的分布式图结构，分布式邻接列表，仅符合分布式顶点列表图概念，因此只有将其包装在合适的适配器（例如 vertex_list_adaptor）中时，才能将它与这些算法一起使用。

定义位置

<boost/graph/distributed/dehne_gotz_min_spanning_tree.hpp>

参数

输入Graph& g

图类型必须是顶点列表图和分布式边列表图的模型。

输入/输出WeightMap weight

权重映射必须是分布式属性映射和可读属性映射，其键类型是图的边描述符，值类型是数值类型。

输入/输出OutputIterator out

输出迭代器，MSF 的边将通过它写入。必须能够接受边描述符以进行输出。

输入VertexIndexMap index

从顶点描述符到范围为 [0, num_vertices(g)) 的索引的映射。这必须是可读属性映射，其键类型是顶点描述符，值类型是整数类型，通常是vertices_size_type图的类型。

默认 get(vertex_index, g)

输入/实用程序RankMap rank_map

存储每个顶点的秩，用于维护并查集数据结构。这必须是读/写属性映射，其键类型是顶点描述符，值类型是整数类型。

默认值： 一个iterator_property_map从 STL 向量构建的vertices_size_type图的类型和顶点索引映射。

输入/实用程序ParentMap parent_map

存储每个顶点的父节点（代表），用于维护并查集数据结构。这必须是读/写属性映射，其键类型是顶点描述符，值类型也是顶点描述符。

默认值： 一个iterator_property_map从 STL 向量构建的vertex_descriptor图的类型和顶点索引映射。

输入/实用程序SupervertexMap supervertex_map

存储每个顶点的超顶点索引，用于维护超顶点列表数据结构。这必须是读/写属性映射，其键类型是顶点描述符，值类型是整数类型。

默认值： 一个iterator_property_map从 STL 向量构建的vertices_size_type图的类型和顶点索引映射。

`dense_boruvka_minimum_spanning_tree`

namespace graph {
  template<typename Graph, typename WeightMap, typename OutputIterator,
           typename VertexIndexMap, typename RankMap, typename ParentMap,
           typename SupervertexMap>
  OutputIterator
  dense_boruvka_minimum_spanning_tree(const Graph& g, WeightMap weight_map,
                                    OutputIterator out,
                                    VertexIndexMap index,
                                    RankMap rank_map, ParentMap parent_map,
                                    SupervertexMap supervertex_map);

  template<typename Graph, typename WeightMap, typename OutputIterator,
           typename VertexIndex>
  OutputIterator
  dense_boruvka_minimum_spanning_tree(const Graph& g, WeightMap weight_map,
                                    OutputIterator out, VertexIndex index);

  template<typename Graph, typename WeightMap, typename OutputIterator>
  OutputIterator
  dense_boruvka_minimum_spanning_tree(const Graph& g, WeightMap weight_map,
                                    OutputIterator out);
}

描述

dense Boruvka 分布式最小生成树算法是 Boruvka 顺序 MST 算法的直接并行化。该算法首先从每个顶点创建一个超顶点。然后，在每次迭代中，它找到与每个顶点关联的最小权重边，沿这些边折叠超顶点，并删除所有自环。顺序算法和并行算法之间唯一的区别是，并行算法执行全归约操作，以便所有进程都具有全局最小边集。

与其他三种算法不同，此算法通过所有进程上的输出迭代器发出最小生成森林中的完整边列表。因此，在并行化顺序 BGL 程序时，它可能比其他算法更有用。

复杂度

分布式算法需要 O(log n) BSP 超步，每个超步都需要 O(m/p + n) 时间和每个进程 O(n) 通信量。

性能

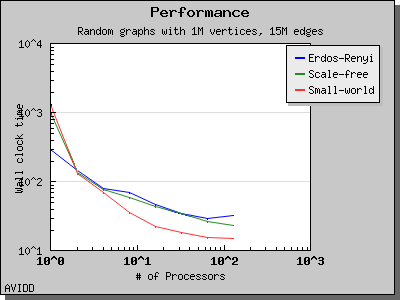
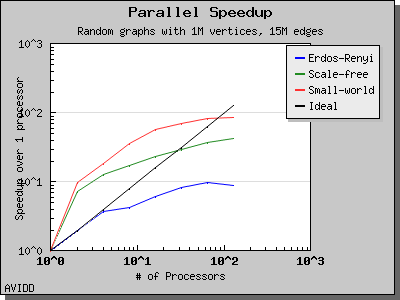
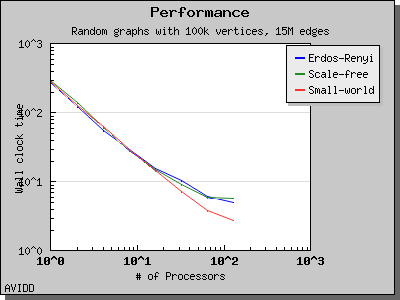
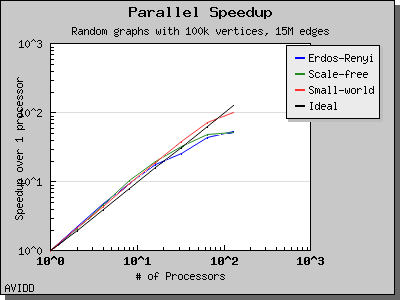
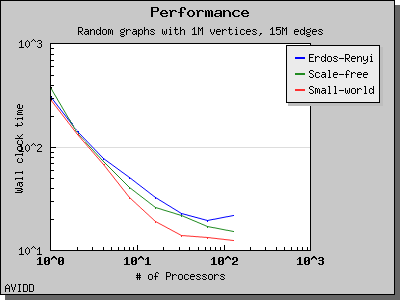
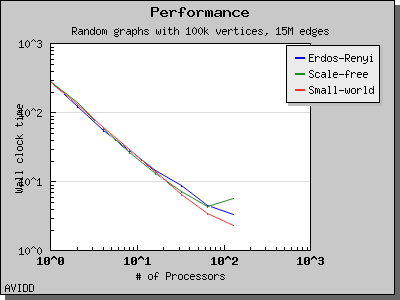
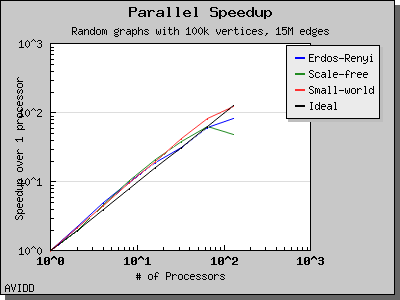
以下图表说明了此算法在各种随机图上的性能。我们看到，对于稠密图，该算法可以很好地扩展到 64 或 128 个处理器，具体取决于图的类型。但是，对于稀疏图，当处理器数量超过 m/n 时，即平均度（对于此图为 30）时，性能会逐渐下降。这种行为是算法所预期的。

`merge_local_minimum_spanning_trees`

namespace graph {
  template<typename Graph, typename WeightMap, typename OutputIterator,
           typename VertexIndexMap>
  OutputIterator
  merge_local_minimum_spanning_trees(const Graph& g, WeightMap weight,
                                     OutputIterator out,
                                     VertexIndexMap index);

  template<typename Graph, typename WeightMap, typename OutputIterator>
  inline OutputIterator
  merge_local_minimum_spanning_trees(const Graph& g, WeightMap weight,
                                     OutputIterator out);
}

描述

合并本地 MST 算法的工作原理是计算每个进程上存储的边的最小生成森林。然后，进程沿树合并其边列表。子节点停止参与计算，但父节点根据新获取的边重新计算 MSF。在最后一轮中，树的根计算全局 MSF，它通过树接收来自每个其他进程的候选边。

复杂度

此算法需要 O(log_D p) BSP 超步（其中 D 是树中子节点的数量，目前固定为 3）。每个超步需要 O((m/p) log (m/p) + n) 时间和每个进程 O(m/p) 通信量。

性能

以下图表说明了此算法在各种随机图上的性能。该算法仅在非常稠密的图上才能很好地扩展，在非常稠密的图中，大部分工作在初始阶段完成，而在后期阶段工作量很少。

`boruvka_then_merge`

namespace graph {
  template<typename Graph, typename WeightMap, typename OutputIterator,
           typename VertexIndexMap, typename RankMap, typename ParentMap,
           typename SupervertexMap>
  OutputIterator
  boruvka_then_merge(const Graph& g, WeightMap weight, OutputIterator out,
                     VertexIndexMap index, RankMap rank_map,
                     ParentMap parent_map, SupervertexMap
                     supervertex_map);

  template<typename Graph, typename WeightMap, typename OutputIterator,
           typename VertexIndexMap>
  inline OutputIterator
  boruvka_then_merge(const Graph& g, WeightMap weight, OutputIterator out,
                      VertexIndexMap index);

  template<typename Graph, typename WeightMap, typename OutputIterator>
  inline OutputIterator
  boruvka_then_merge(const Graph& g, WeightMap weight, OutputIterator out);
}

描述

此算法将 Boruvka 步骤和本地 MSF 合并步骤结合在一起，以实现比任何一种算法单独使用更好的渐近性能。它首先执行 Boruvka 步骤，直到仅剩下 n/(log_d p)^2 个超顶点，然后通过对剩余的边和超顶点执行本地 MSF 合并来完成 MSF 计算。

复杂度

此算法需要 log_D p + log log_D p BSP 超步。每个超步所需的时间取决于正在执行的超步的类型；有关详细信息，请参阅分布式 Boruvka 或合并本地 MSF 算法。

性能

`boruvka_mixed_merge`

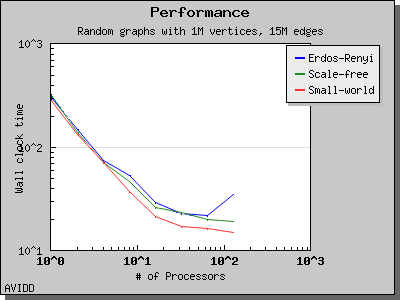
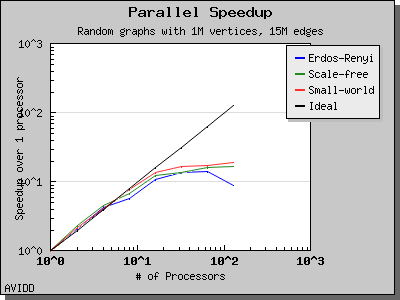
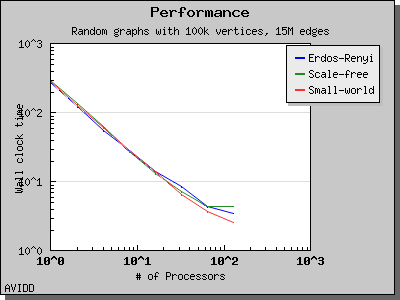
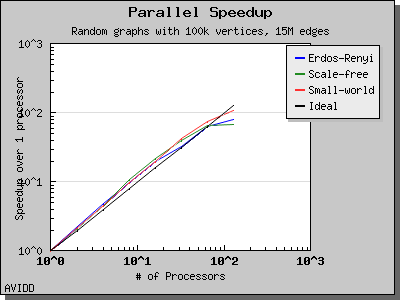
namespace {
  template<typename Graph, typename WeightMap, typename OutputIterator,
           typename VertexIndexMap, typename RankMap, typename ParentMap,
           typename SupervertexMap>
  OutputIterator
  boruvka_mixed_merge(const Graph& g, WeightMap weight, OutputIterator out,
                      VertexIndexMap index, RankMap rank_map,
                      ParentMap parent_map, SupervertexMap
                      supervertex_map);

  template<typename Graph, typename WeightMap, typename OutputIterator,
           typename VertexIndexMap>
  inline OutputIterator
  boruvka_mixed_merge(const Graph& g, WeightMap weight, OutputIterator out,
                      VertexIndexMap index);

  template<typename Graph, typename WeightMap, typename OutputIterator>
  inline OutputIterator
  boruvka_mixed_merge(const Graph& g, WeightMap weight, OutputIterator out);
}

描述

此算法将 Boruvka 步骤和本地 MSF 合并步骤结合在一起，以实现比任何一种方法单独使用更好的渐近性能。在每次迭代中，该算法首先执行 Boruvka 步骤，然后合并基于超顶点图计算的本地 MSF。

复杂度

此算法需要 log_D p BSP 超步。每个超步所需的时间取决于正在执行的超步的类型；有关详细信息，请参阅分布式 Boruvka 或合并本地 MSF 算法。但是，当图足够稠密时，即 m/n >= p 时，该算法是通信可选的（总体上需要 O(n) 通信量）。

性能

选择 MST 算法

Dehne 和 Gotz 报告 [DG98] 在评估这四种算法时结果不一。在所有情况下，没有哪种特定算法明显优于其他算法。然而，渐近最佳算法 (boruvka_mixed_merge) 在他们的测试中，其性能似乎比其他基于合并的算法更差。以下性能图表说明了这四种最小生成树实现的性能。

总的来说，dense_boruvka_minimum_spanning_tree对于我们测试的图，提供了最一致的性能和可扩展性。此外，它可能更适合正在并行化的顺序程序，因为它通过每个进程中的输出迭代器发出完整的 MSF 边列表。

稀疏图上的性能

稠密图上的性能

作者：Douglas Gregor 和 Andrew Lumsdaine

[DG98]

(1, 2) Frank Dehne 和 Silvia Gotz. 最小生成树的实用并行算法。载于可靠分布式系统研讨会，第 366--371 页，1998 年。